
Study Atomic Cooling
- To prepare Bose-Einstein condensate you need many things to work together. To debug the complicated system you will need to understand each cooling technique involved. Ask yourselves next questions to see if you know enough!
- Last Updated: Jun 30, 2024
- Published: Mar 15, 2023
Table of Contents
Resources
- Inguscio, M., & Fallani, L. (2013). Atomic Physics: Precise Measurements and Ultracold Matter. https://doi.org/10.1093/acprof:oso/9780198525844.001.0001, chapters 2-3
- Taras Hrushevskyi, Quantum gas apparatus for Bose-Einstein condensation of 87Rb, MSc Thesis (Jan 2017).
- Lukin’s notes on atomic physics, chapter 8
- Foot, C. J. (2004). Atomic physics (Vol. 7). OUP Oxford. Chapter 9.
- Metcalf, H. J., & Van der Straten, P. (1999). Laser cooling and trapping. Springer Science & Business Media.
Questionnaire
We will start with discussing different cooling mechanisms and see how can they all be put together to prepare BEC.
Magneto-optical trap
- Optical part
- What is a basic idea behind optical laser cooling? The basic idea involves using laser light to reduce the kinetic energy of atoms. When an atom absorbs a photon from a laser beam, it gains momentum in the direction of the photon. Subsequent spontaneous emission of photons occurs in random directions, resulting in a net loss of kinetic energy and cooling of the atoms. Photon carries small momentum, so many absorption and reemission cycles need to happen to change atom velocity.
- Why laser is red-detuned? How far to detune?
As we said above atom gets net momentum from the photons through absorption/reemission process. To slow the atom down, we need it to get kicks in a specific direction, opposite to its movement. This could be done by tuning the laser frequency slightly below an atomic resonance (red-detuned). In this case, atoms moving towards the laser will preferentially absorb photons, leading to a reduction in their velocity in that direction. Check diagram.
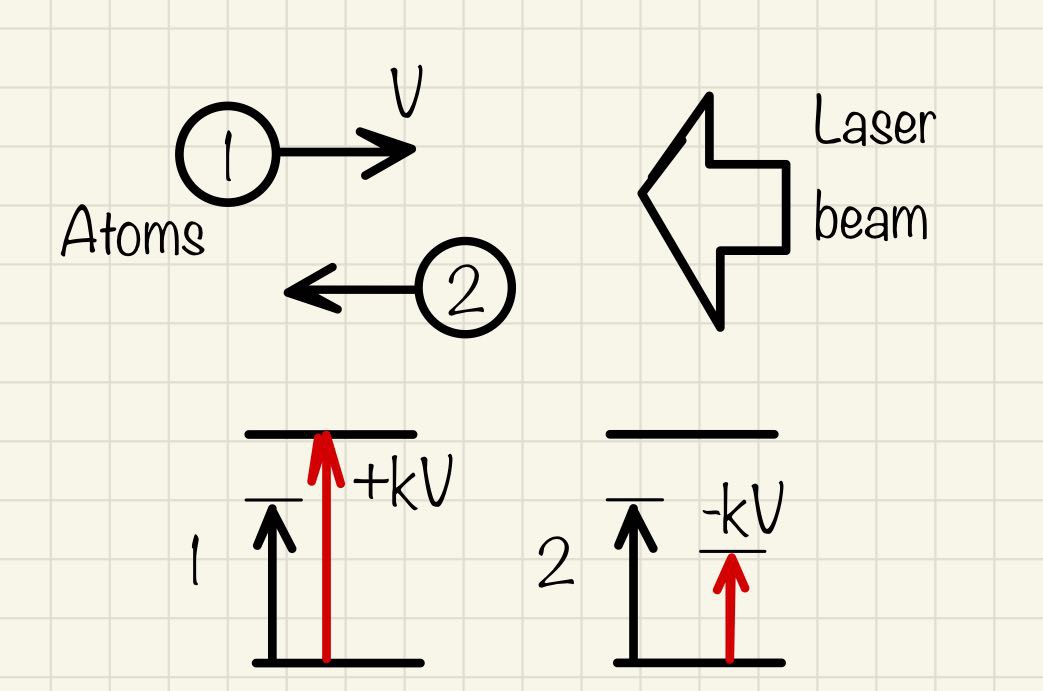
Atom '1' moves toward the beam and sees laser frequency 'higher' or more resonant iwth its transition. For the '2' atom, which is co-propagating with the beam, the laser is further detuned and less likely to be absorbed. - Which directions the laser should be sent through? How to do this?
To achieve three-dimensional cooling, six laser beams are used, with two beams aligned along each of the three spatial axes (x, y, z). Each pair of counter-propagating beams provides cooling in one direction, ensuring that atoms are cooled in all spatial directions. A laser can be split into 6 beams free-space and directly send them. A neat alternative is to have a fiber beam-splitter, which has one-to-many options. Of course, this simplicity comes at the cost of insertion losses, polarization fluctuations, and unability to tune splitting, which is fixed upon manufacturing.
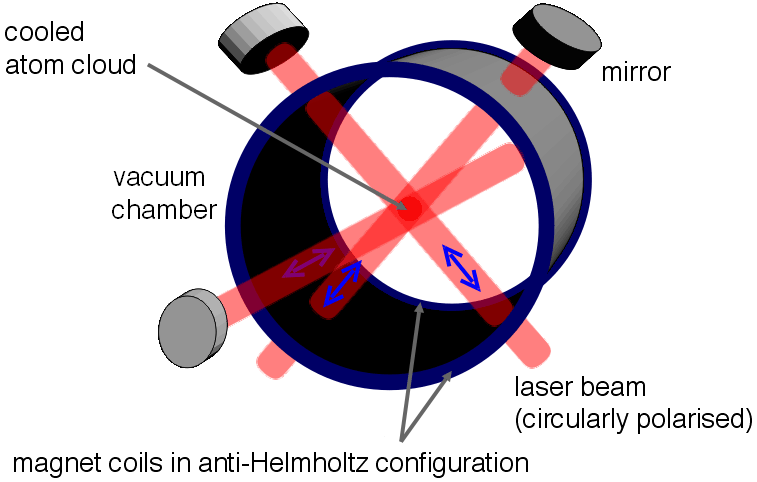
From wiki. Beams can be sent from three directions and then backreflected to have the rest of beams. - Which frequency to choose for the cooling laser and why?
One would think that any resonance would work. Although if we remember that alkali atoms have multiple metastable levels. Thus during the cooling process we want to exclude atoms from falling into a dark state, which is not participating in cooling process. It is worth exploring ‘closed’ transition, for which spontaneous emission to unwanted levels is suppressed via selection rules.
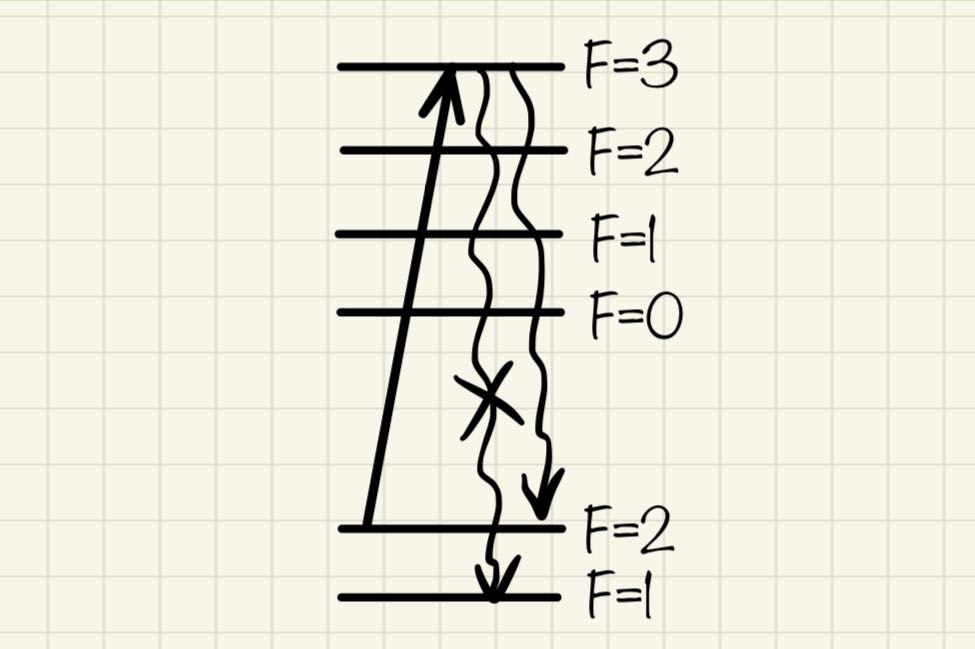
Here I specifically give structure of D2 line of alkali atoms with nuclear spin I=3/2. If atom is excited from F=2 to F'=3 level, than spontaneous emission to F=1 level is suppressed due to selection rules. - Why do we need two lasers? Describe all possible loss mechanisms Atoms still can decay from F=2 to F=1, via spontaneous decay. The second path is to spontaneously decay from F=3 to F=2 despite selection rules; the probability is low but it is not zero. The third path to escape from cooling process is to transition from F=2 to F’=2 under applied cooling laser. This is an allowed transition, it will be less probable due to detuning, but with high cooling power and many absorption/reemission cycles still results in some atoms to lend onto a dark F=1 state. All these losses can be individually accounted, although they just result in atoms stopping to interact with cooling light and lending onto F=1 level. To solve this problem people introduce repumping laser, which brings them back to F=2 level.
- Central frequencies of two lasers? As we discussed cooling laser needs to be slightly red-detuned from an optical transition. Specifically for Rubidium 87 it is cenetered on the D2 line, transition F=2 ↔ F’=3, detuned by 18 MHz (
- Which power of the beam we need for both lasers? The power of the laser beams required for cooling depends on the atomic species and the specifics of the cooling transition. Generally, the power is chosen such that the intensity of the laser beams is close to or below the saturation intensity of the atomic transition. For rubidium-87 (Rb87), the saturation intensity for the D2 line is about 1.6 mW/cm², and typical cooling beams have intensities of a few times this value. Of course the total power will depend on beam waists. I typically seen beam diameters of 1-2 cm, with 20 mW of cooling laser per beam and 10 mW of repump power, but to some extent the more the merrier.
- Magnetic part
- Why do we need magnetic coils? We discussed the basics of the force which slows down atoms due to absorption/reemission of cooling laser. Magnetic coils are used to create a trapping potential. The magnetic field gradient ensures that atoms experience a position-dependent restoring force due to the Zeeman effect, which helps to confine the atoms in the center of the trap and enhances the cooling efficiency. Thus people use two coils in anti-Helmholtz configuration to choose zero trapping point.
- Field of anti-Helmholtz configuration and role it plays in cooling? We just said that additional field gradient createds position dependent force. The configuration for the ‘full’ magneto-optical trap includes two- orthogonally polarized beams propagating towards each other; magnetic field which is zero in a center of the trap and increases as you go away from the center, while it has different signs from two sides of the zero.
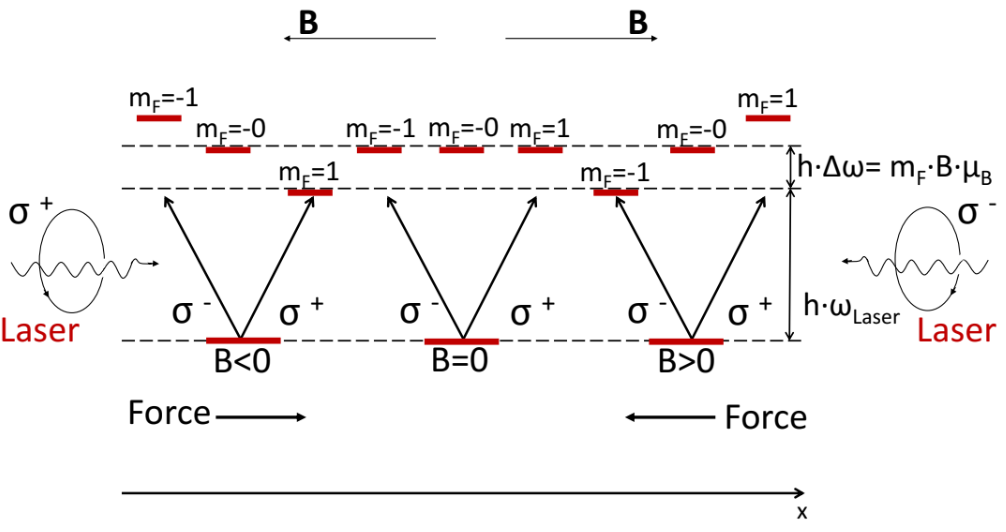
Figure is taken from Taras's thesis, Figure 2.4. - Typical magnetic fields and currents? We apply around 20-25 A of current through our coils, which creates a field gradient with magnitude of 0.197 G/(cm*A) in radial direction and 0.42 G/(cm*A) in vertical direction. With this parameters we have approximately 5 and 10.5 G/cm during MOT stage; 84 and 176 G/cm during magnetic trapping stage (discussed below).
- Why do we need bias fields?
It is difficult to perfectly match center of magnetic trap and intersection of six beams. By applying bias magnetic field in three directions, we can compensate for imperfections.Once again we want to promote absorption of a photon which will give us a kick in the coorect direction, which is towards the zero magnetic field. If our atom moves along our x axis
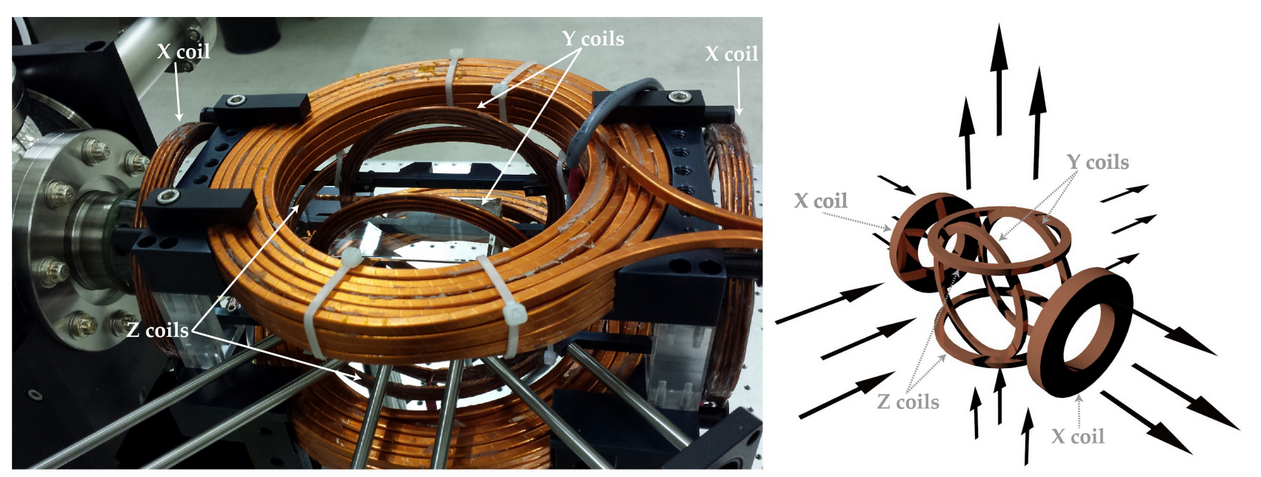
Figure is taken from Taras's thesis, Figure 3.9. Bias coils together with 3D-MOT/MT mounted on the cage around glass cell(left). Arrows indicates magnetic field direction for each pair of coils if positive voltage is applied from power supplies.
- Overall performance of MOT
- What is the lowest temperature we can get to?
The lowest temperature achievable in Doppler cooling is given by the Doppler limit:
- What makes the final temperature non-zero? The final temperature is non-zero due to several factors:
- Recoil Limit: Even at the Doppler limit, the random recoils from spontaneous emissions impart kinetic energy to the atoms, setting a lower bound on the achievable temperature.
- Laser Intensity and Frequency Noise: Fluctuations in laser intensity and frequency can introduce heating effects.
- Laser Beam Imperfections: Non-ideal beam profiles and alignments can lead to less effective cooling.
- Residual Magnetic Fields: Imperfect magnetic field control can result in non-ideal trapping and heating. While Doppler cooling provides significant cooling, other techniques such as sub-Doppler cooling (e.g., Sisyphus cooling) can achieve temperatures below the Doppler limit by exploiting additional mechanisms.
- How many atoms? Optical depths.
- What is the lowest temperature we can get to?
The lowest temperature achievable in Doppler cooling is given by the Doppler limit:
SubDoppler cooling
- Basic idea behind It: Sub-Doppler cooling techniques take advantage of the multilevel structure of atoms and polarization gradients of the laser light to achieve temperatures lower than the Doppler limit. One common method is Sisyphus cooling, which involves optical pumping in a spatially varying light field, causing atoms to lose kinetic energy as they move through regions of varying potential energy created by the light’s polarization patterns. Mamba jamba for now?
- Polarizations used for two beams:
Sisyphus cooling uses two orthogonal polarizations, either “lin ⊥ lin” (linear orthogonal polarization) or “σ+ - σ-” (circular opposite polarization). In the “lin ⊥ lin” configuration, the polarization of one laser beam is linear and orthogonal to the polarization of the counter-propagating beam.
If we look into spatial variation of polarizarion of two counter-propagating fields, where we set to orthogonal linear polarizations along x and y:
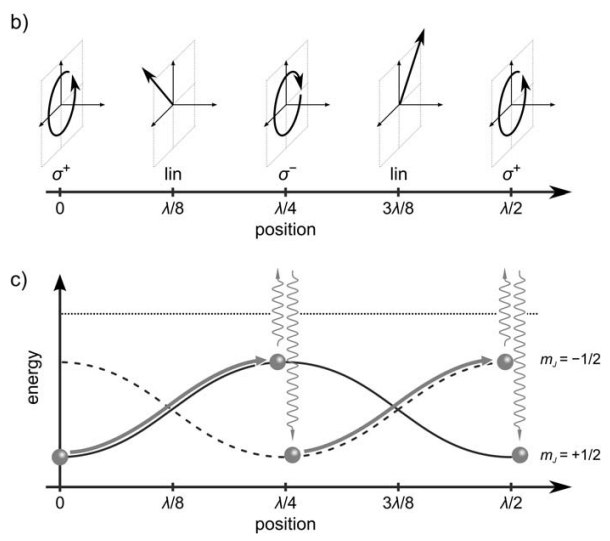
Figure 2.11 from a book *Inguscio, Massimo, and Leonardo Fallani. Atomic physics: precise measurements and ultracold matter. OUP Oxford, 2013.* - Multilevel atomic structure Besides having polarization gradient we need a multilevel atom, thus nonzero angular momentum is required. Each level will experience ac-Stark shift due to cooling laser, since ac-Stark shift depend on polarization thus energy of different angular momentum sublevels will change spatially. This can be seen on the figure above.
- How cooling happens?
If atom start traveling along the - Incorporating It into Pulse Sequence:
- Preparation: Before starting sub-Doppler cooling, the atoms are usually pre-cooled using Doppler cooling to bring them into the appropriate velocity range for effective sub-Doppler processes.
- Sub-Doppler Cooling Sequence: The sub-Doppler cooling phase is typically applied as a continuous sequence after the Doppler cooling phase. The magnetic field gradients used in Doppler cooling (MOT) are often turned off or reduced to minimize their influence during the sub-Doppler cooling stage.
- Optical Configuration: The cooling laser beams are adjusted to the required polarization configurations (“lin ⊥ lin” or “σ+ - σ-”), and the frequency of the laser light may be tuned slightly closer to resonance to optimize the sub-Doppler cooling process.
- Lowest Temperature Achievable:
The lowest temperature achievable in sub-Doppler cooling is limited by the recoil temperature, which is given by:
- What Makes the Final Temperature Non-Zero:
- Recoil Limit: Even at the lowest temperatures achievable by sub-Doppler cooling, the atoms experience recoil from the absorption and spontaneous emission of photons, setting a fundamental lower limit on temperature.
- Intensity Fluctuations: Variations in the intensity of the cooling lasers can lead to heating effects.
- Laser Frequency Noise: Noise in the frequency of the lasers can reduce the cooling efficiency and lead to heating.
- Beam Alignment and Quality: Imperfections in the laser beam alignment and quality can result in less effective cooling.
- Residual Magnetic Fields: Even small magnetic fields can influence the energy levels of the atoms, leading to non-ideal cooling. Sub-Doppler cooling techniques, such as Sisyphus cooling, can achieve temperatures well below the Doppler limit, providing highly efficient cooling for applications requiring ultra-cold atomic samples.
Two ways to trap atoms
Magnetic trapping
- Describe force/potential due to magnetic field:
Atoms with non-zero magnetic dipole moment interact with magnetic field, that potential energy
- Which atoms are not trappable?
Atoms in states with zero total angular momentum (such as (J = 0) states) or in states where the magnetic moment
- What are high/low-field seeking states?
- Low-Field Seeking States: These are states where the atom is repelled by regions of high magnetic field strength and attracted to regions of low magnetic field strength (e.g., (m_F > 0) in a weak field).
- High-Field Seeking States: These are states where the atom is attracted to regions of high magnetic field strength and repelled by regions of low magnetic field strength (e.g., (m_F < 0) in a weak field).
- How big current we need to create potential well of specific height (formula)?
The magnetic field gradient
- Which currents do we use in our setup? For compression and for holding atoms? We found experimentally that 65 A of current is enough to hold atoms against gravity and we ramp it up to 420 A in order to compress cloud and to achieve effective cooling (Described below).
- How do we use magnetic trap to check background pressure? Magnetic traps can be used to check background pressure by monitoring the lifetime of trapped atoms. Higher background gas pressure results in more frequent collisions between trapped atoms and gas molecules, leading to increased loss rates. By measuring the decay of the trapped atom population, we can infer the background pressure.
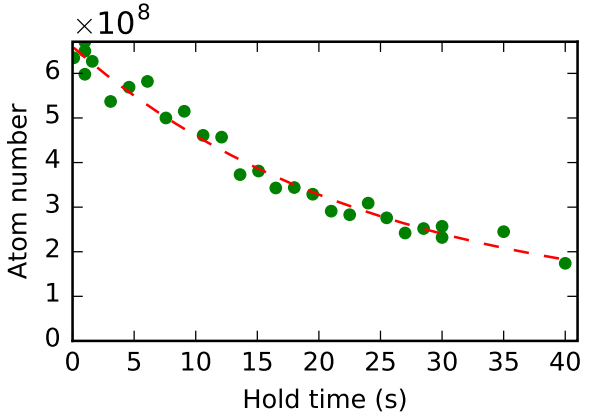
Figure is taken from Taras's thesis, Figure 4.7. We check estimate lifetime of atoms in a compressed trap to be arouns 24 seconds. - What are Majorana losses? Majorana losses occur when atoms in a magnetic trap pass through regions where the magnetic field is very weak or zero, causing a non-adiabatic transition between magnetic sublevels. In such regions, the quantization axis of the magnetic field changes rapidly, and if an atom’s spin does not follow the changing field, it can be lost from the trap. This effect is particularly problematic in traps with zero magnetic field at the center, such as quadrupole traps.
- Describe force/potential due to magnetic field:
Atoms with non-zero magnetic dipole moment interact with magnetic field, that potential energy
Optical dipole trap
- What is an optical dipole trap? If an applied field is far-detuned from resonance, an imaginary part of susceptibily dominates in atomic response. This results in appearence of force due to AC-Stark potential
- What is crossed-beam dipole trap In order to trap atoms people cross two focused beams at 90 degree angle. If we have a single beam atoms won’t collect in a small area. While we are crossing two beams with waists of approximately 100 um, we can receive trapping in a small area where two beams overlap and create stronger potential.
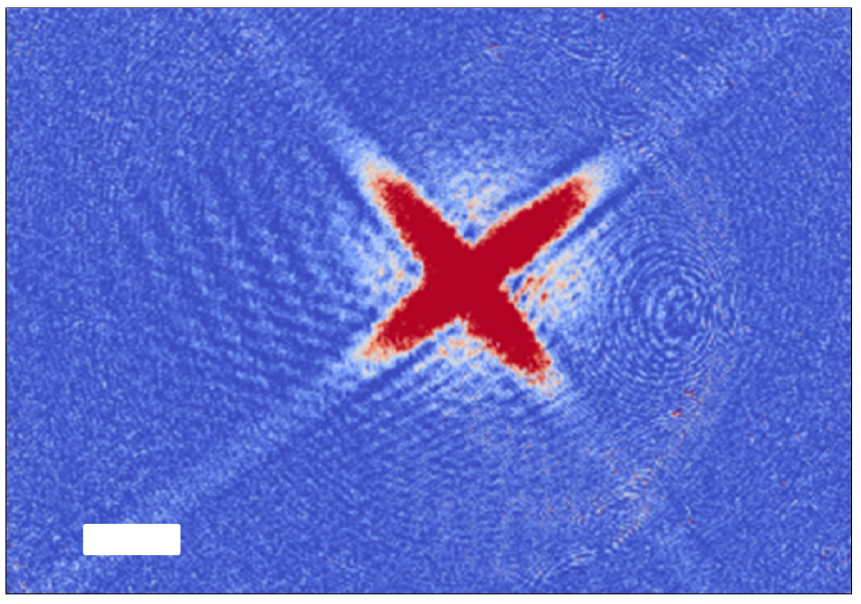
Figure is taken from Taras's thesis, Figure 3.24. Absorption images of the atomic cloud just after transfer into the ODT beams. White scale bare = 100 µm. - How not to create a standing wave? We know that if we overlap two laser beams they would interfere, although we don’t want to create any nodes or antinodes across our trapping potential. Thus we take two measures to prevent against interference: we use orthogonal polarizations for two beams and we use a laser with very bad linewidth (approximately 1 nm).
- How much power in each beam vs potential height?
From this reference, the trap depth is given by
- Trap frequencies and ways to measure?
- What is an optical dipole trap? If an applied field is far-detuned from resonance, an imaginary part of susceptibily dominates in atomic response. This results in appearence of force due to AC-Stark potential
Cooling in a trap
RF knife evaporative cooling
- What is the main idea behind it?
Let us assume that we have two magnetic sublevels
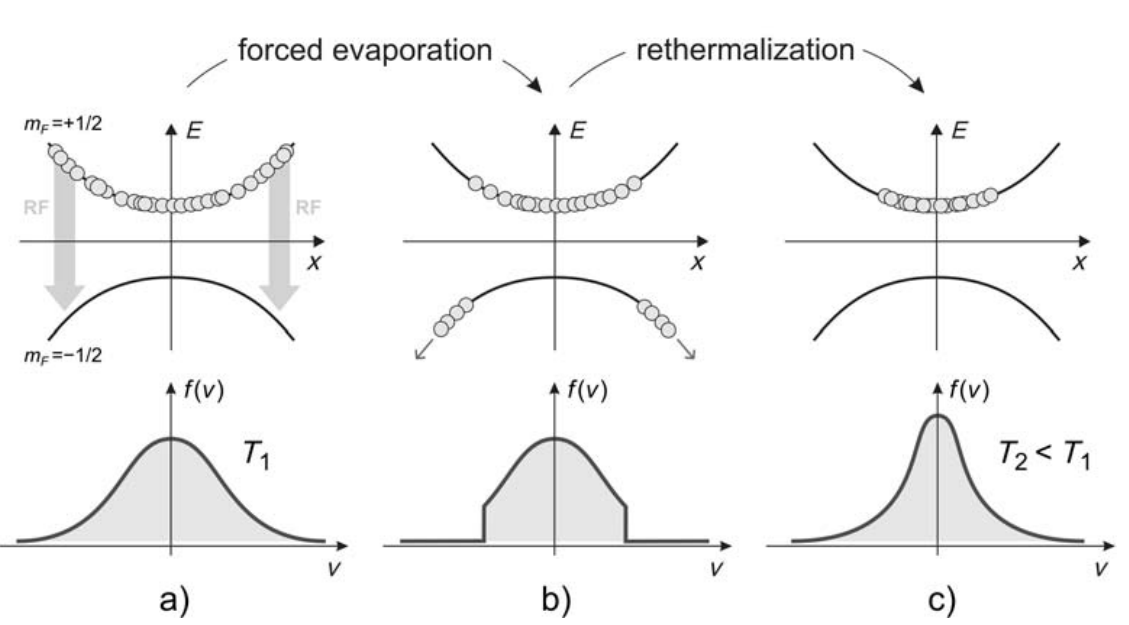
Figure 3.4 from a book Inguscio, Massimo, and Leonardo Fallani. Atomic physics: precise measurements and ultracold matter. OUP Oxford, 2013. - Importance of scattering length Reethermalization. We ramp current up first to high values in order to increase atomic density and collision rate.
- Which frequencies we use? We sweep frequencies starting from 20 MHz down to 0.7 MHz during 5 seconds. We measure temperatures at each step along the way.
- How much power do we need?
ODT evaporative cooling
- What is the main idea behind it? Light and atoms interact through susceptibility
- How do we ramp power down?
- Which temperatures we get?
BEC preparation
Combine all of the above together
- Which different mechanisms we combine to produce BEC?

Here is step-by step cooling which produces BEC in our system - Let’s summarize what are step’s durations, which atom numbers, and temperatures are we getting? Here is a table with approximate temperatures and atom number at each stage.
- Any auxiliary steps we need to have?
- Summarize which lasers we need to prepare BEC, their central wavelengths and powers.
Measurement
- How can we verify that we prepared an ensemble
- How do we prove that it is a BEC
- What not desruptive measurements
- Stern-Gerlach measurement
- Coherence measurements
Some technical issues to produce BEC
- Ultra-high vacuum and 2D MOT and push beam
- Mayorana losses and ways to overcome it to use magnetic trapping for cooling
- What are the conditions at which atoms condense?
- What is the difference between BEC and thermal cloud?
- Which experiments do you need BEC for?
More ways to cool
- Raman and sideband cooling
- Gray molasses (cooling for potassium)
- Preparing BEC on a chip
- What if we have fermions
- What if I want ultracold molecules?
Answers: in progress
Coming soon…