
Study quantum basics
- This is a list of topics which are unsorted at this point, but which give a basis to start your research in quantum domain. This is a way to help me organize thoughts on topics, saying what I know and what I am willing to understand
- Last Updated: May 20, 2024
- Published: Mar 15, 2023
Table of Contents
Quantum computing: answers
Existing quantum computers
- Which physical realizations of quantum computers exist? Current physical realizations include
- superconducting circuits,
- trapped ions,
- neutral atoms,
- photonics,
- topological qubits using anyons.
- How many qubits are there? How many do we need?
- What is error correction? Quantum error correction is a set of techniques to protect quantum information from errors induced by decoherence and other imperfections in quantum hardware. It involves encoding logical qubits using multiple physical qubits and implementing error-detecting and error-correcting codes. For this reason currently we need hundreds of physical qubits to realize a single logical qubit.
Qudit
- What is a qubit?
A qubit is the fundamental unit of quantum information, representing a quantum version of classical bits. It can exist in a superposition of states, allowing for parallel processing of information. Mathematically it could be written as follows:
- How qubit compares to a classical bit? Unlike classical bits that can only exist in states 0 or 1, qubits can exist in a superposition of states, enabling quantum parallelism. Qubits are subject to entanglement, allowing correlations between qubits that classical bits cannot exhibit.
- What is a qudit? In which Hilbert space it leaves?
A qudit is a generalization of a qubit, representing a quantum system with more than two levels.
Bloch sphere
- What is a Bloch sphere? Where do I find my qubit on a Bloch sphere?
The Bloch sphere is a geometric representation of the state space of a qubit. It is a unitary sphere. A qubit state is represented by a point on the surface of the Bloch sphere.In a sense an infinite plane is wrapped or mapped onto a sphere, this is called stereographic projection. How to perform this is nicely described here.
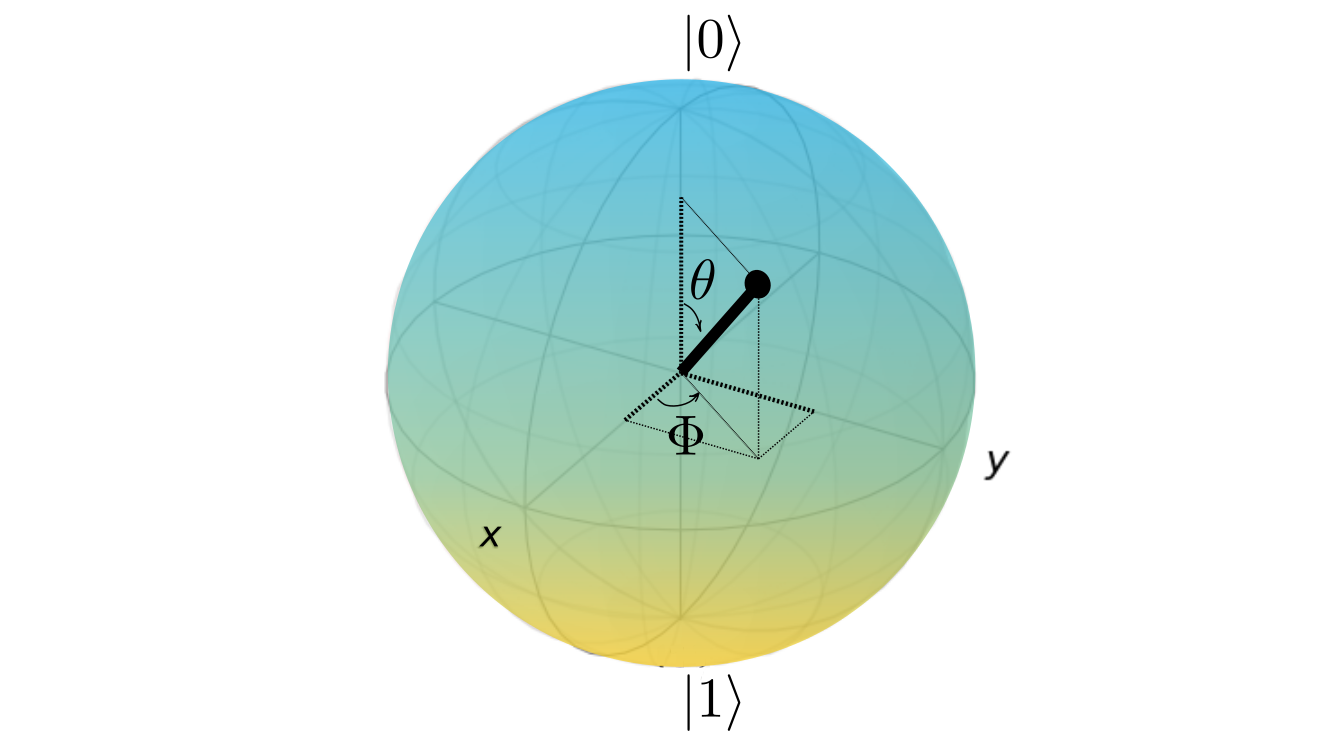
Bloch sphere. - Main axis of a Bloch sphere
The main axis are Pauli matrices eigenvectors.If qubit is oriented along Z axis, we find it either in 0 or 1 state. On equator qubit is in equal superposition between two levels, with an arbitrary phase.
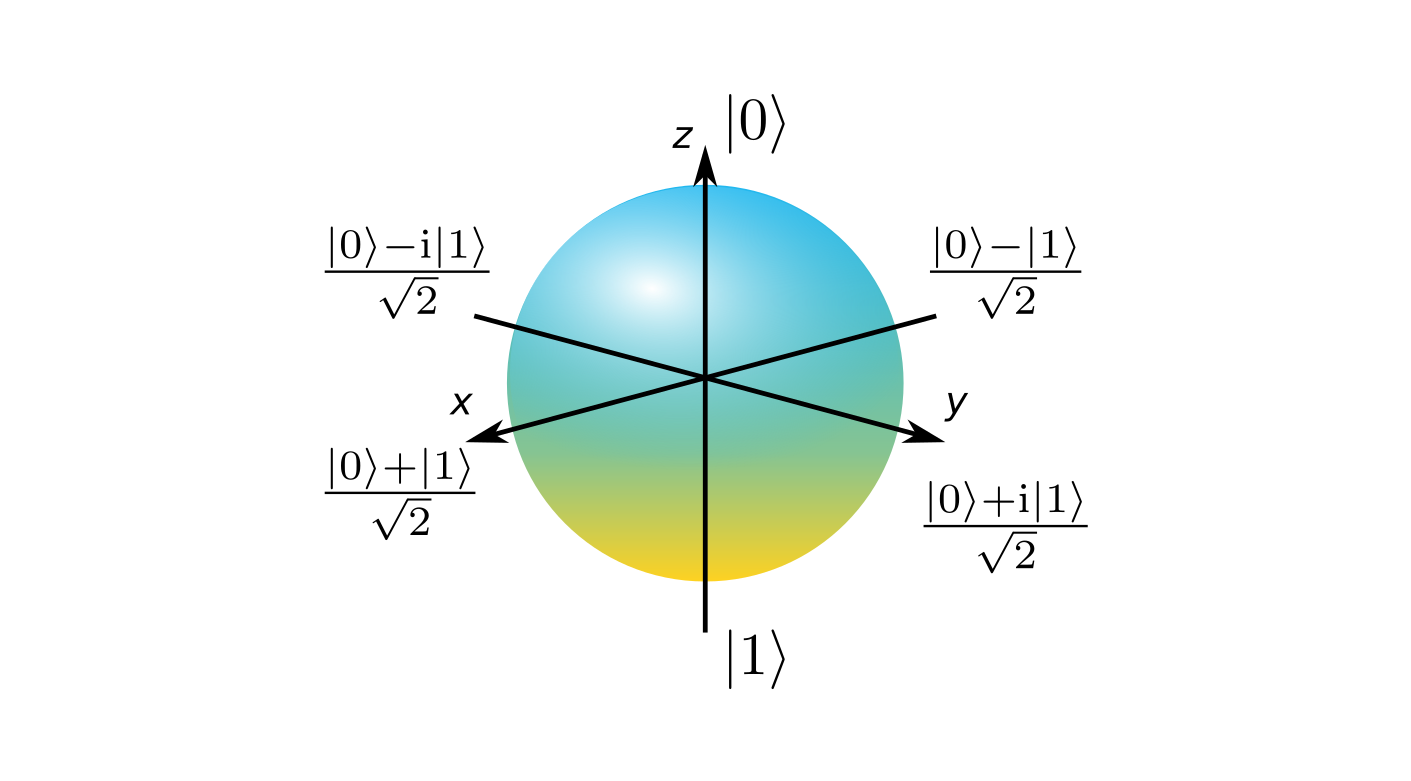
The main axis are Pauli matrices eigenvectors. - How to represent mixed states? If the system is not in a pure state, so we are working with a density matrix. In this case the qubit will be anywhere within a Bloch sphere. From wikipedia:
Mixed states are represented by an interior point. Thus, the purity of a state can be visualized as the degree to which the point is close to the surface of the sphere. The completely mixed state of a single qubit is represented by the center of the sphere.
- How to represent a qudit on a Bloch sphere? If you are working with a qudit, you can still use a sphere. Although representation will be a constellation of stars. Once again a nice reference is this blog.
Basic gates
- Rotation under Pauli matrices Single-qubit gates include rotations under Pauli matrices (X, Y, Z). A rotation by an angle θ about the X-axis is represented by the matrix exp(-iθX/2), and similarly for Y and Z.
- How to perform an arbitrary rotation Any arbitrary single-qubit rotation can be performed using a combination of rotations under Pauli matrices. For example, the single-qubit gate Rx(θ) can be decomposed into rotations around the X, Y, and Z axes.
- Single-qubit gates Common single-qubit gates include Hadamard (H), phase (S), and pi/8 (T) gates, each performing specific rotations on the Bloch sphere.
- Two-qubit gates Examples of two-qubit gates include the CNOT gate, which performs a controlled-X operation based on the state of another qubit.
Universal quantum computer
- DiVincenzo criteria DiVincenzo criteria are a set of requirements for building a practical quantum computer. Criteria include a scalable physical qubit array, universal gate set, efficient qubit initialization, long qubit coherence times, and a faithful qubit measurement.
- Set of universal gates A universal gate set is a set of quantum gates that can be combined to approximate any unitary transformation. Examples include the Hadamard, phase, and CNOT gates.
Quantum advantage
- How much information can I save on a single qubit? A single qubit can store an infinite amount of classical information when in a superposition of states. In practice, when reading out a single
- Where the advantage comes from? Quantum advantage arises from the ability of quantum systems to process information in parallel through superposition and to exhibit entanglement, enabling correlations not possible with classical systems.
- Lloyd’s theorem Lloyd’s theorem states that a quantum system with n qubits can simulate 2^n classical bits, illustrating the exponential information processing capacity of quantum systems.
- Which algorithms are supposed to have quantum advantage? Quantum algorithms such as Shor’s algorithm (for factoring) and Grover’s algorithm (for search) are believed to provide exponential speedup compared to their best-known classical counterparts.
Preparation of a qubit in an atomic system?
- Select a two-level system within Rb87 sublevels. In rubidium-87 (Rb87), the ground state hyperfine levels can be used as a two-level system for qubit manipulation.
- Which couplings will allow single-qubit gates? Applying external electromagnetic fields, such as microwave or radiofrequency fields, can induce transitions between sublevels, allowing for single-qubit operations.
- What is Hamiltonian and evolution operator for this system
- How rotation of a qubit is performed?
Rotations of a qubit are achieved by applying specific frequency components of an external field, causing transitions between sublevels.
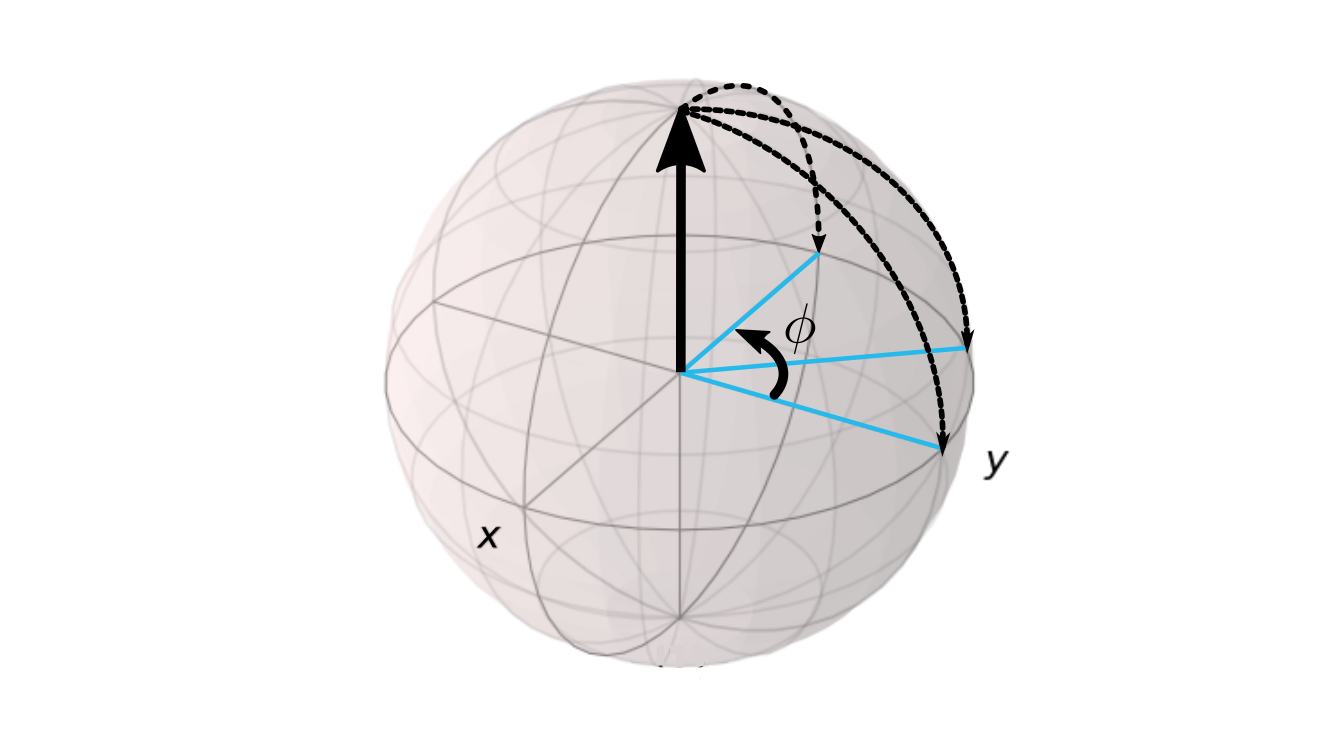
Rotation on a Bloch sphere under applied field.
Measurement of a qubit
- Stern-Gerlach technique The Stern-Gerlach technique involves passing a qubit through an inhomogeneous magnetic field, causing it to align along one of the field’s axes. The resulting measurement provides information about the qubit’s state.
- Basis rotation Basis rotation is a transformation applied to a qubit’s state before measurement to simplify the measurement process. It involves rotating the Bloch vector to align with the measurement basis.
- How much information from each measurement? Each measurement provides a single classical bit of information about the qubit’s state. The outcome is probabilistic, reflecting the quantum nature of the measurement process.
- Step-by-step measurement of a qubit The step-by-step measurement involves preparing the qubit state, applying basis rotations if necessary, and performing the measurement. The result is a classical outcome corresponding to a specific qubit state.